【机器学习】四层人工神经网络拟合二元二次函数
四层人工神经网络拟合二元二次函数
如果想了解人工神经网络,请认真阅读每个字,字字珠玑。😂
核心代码:
、、、、、、、、、、
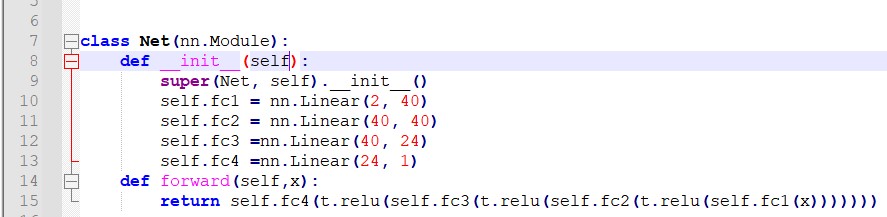
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(2, 40)
self.fc2 = nn.Linear(40, 40)
self.fc3 =nn.Linear(40, 24)
self.fc4 =nn.Linear(24, 1)
def forward(self,x):
return self.fc4(t.relu(self.fc3(t.relu(self.fc2(t.relu(self.fc1(x)))))))
def train(epoch,model,opt,lossfn,tu,tc):
for i in range(1,epoch+1):
tp=model(tu)
loss=lossfn(tp,tc)
opt.zero_grad()
loss.backward()
opt.step()
if i % 10 == 0 or i == 1:
print('Epoch %d, Loss %f' % (i, float(loss)))
return model
def f(x,x2):
return x**2+x2
PATH = "cyNN.pt"
cyNN=t.load(PATH)
cyNN.eval()
opt=optim.Adam(cyNN.parameters(),lr=1e-7)
、、、、、、、、、、
我们这个模型拟合的函数是:f(x,x2)=x^2+x2
最最重要的核心调用框架
神经网络解释
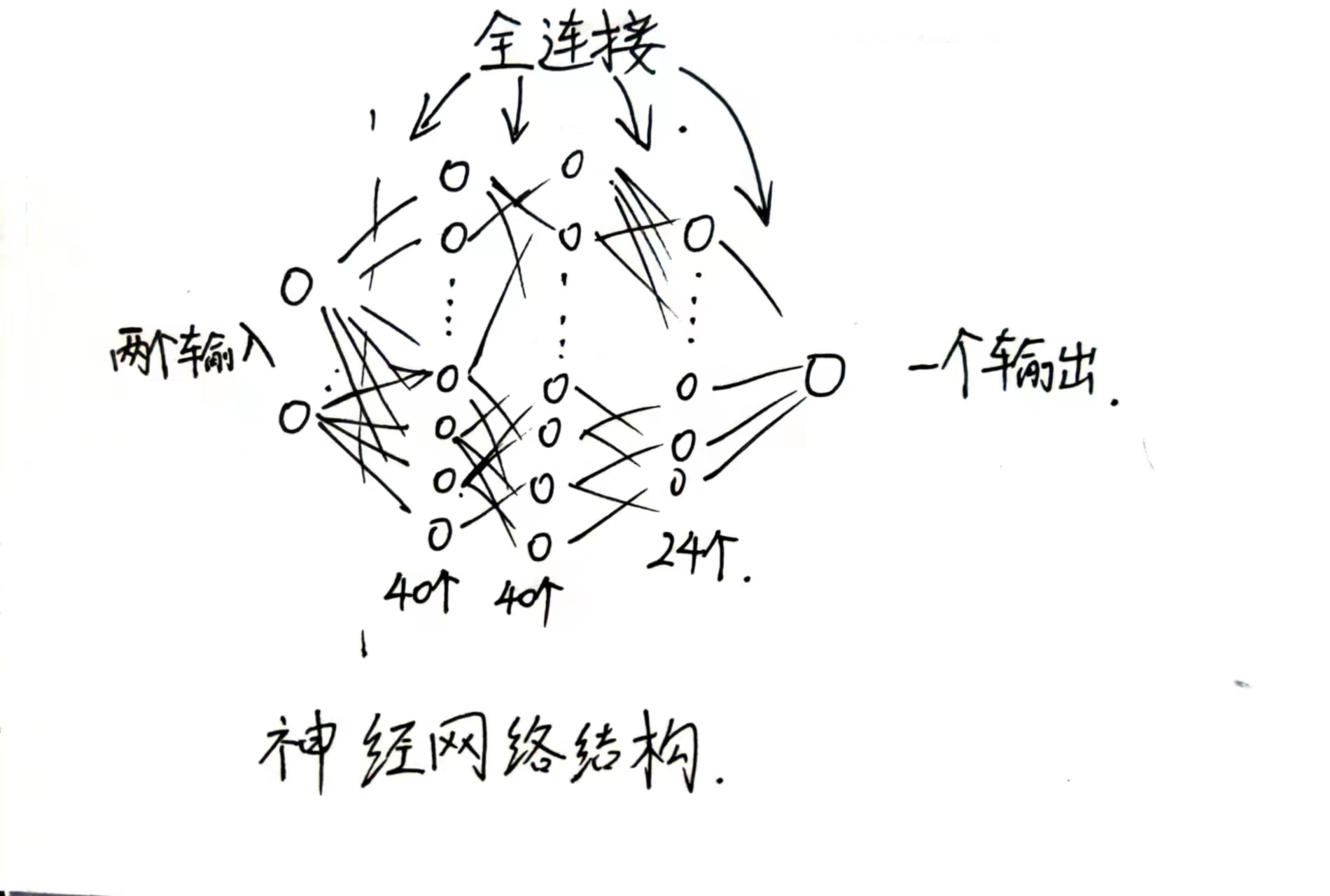
这是一个四层人工神经网络,拟合二元二次函数。
输入层有两个神经元,输出层有一个神经元,中间两层各有40个神经元,最后一层有24个神经元。激活函数使用的是ReLU,优化器使用的是Adam,学习率为1e-7,损失函数使用的是MSELoss。
输入层:2个神经元 (表示两个自变量)
隐藏层1:40个神经元
隐藏层2:40个神经元
隐藏层3:24个神经元
输出层:1个神经元 (表示一个因变量)
激活函数:ReLU (线性整流函数)
优化器:Adam
学习率:1e-7
损失函数:MSELoss(即均方误差,也就是绝对误差的平方)
结构图
(一目了然这个属于是=。=)
激活函数
这个激活函数采用的是ReLU,即线性整流函数,公式如下:
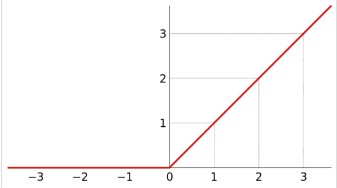
这个函数的特点是,当x>0时,y=x,当x<0时,y=0,这样就可以避免梯度消失的问题。同时,这个函数非常简单(数学公式只是 f(x)=max(0,x)
优化器
这个优化器采用的是Pytorch内置的Adam,这个优化器是基于梯度下降的优化器,它的优点是,不需要精确设置学习率,而且可以自动调整学习率。而且更重要的是它对输入的数据不敏感,不需要对数据进行归一化处理。(可以同时处理不同量级的输入数据,例如同时处理0.1和10000的数据)
损失函数
这个损失函数采用的是MSELoss,即均方误差,也就是绝对误差的平方。没啥好说的。
测试环节
这里我用了一个简单的测试方法,就是随机输入二元二次函数的数据,然后用这个神经网络进行拟合,看看拟合的效果如何。
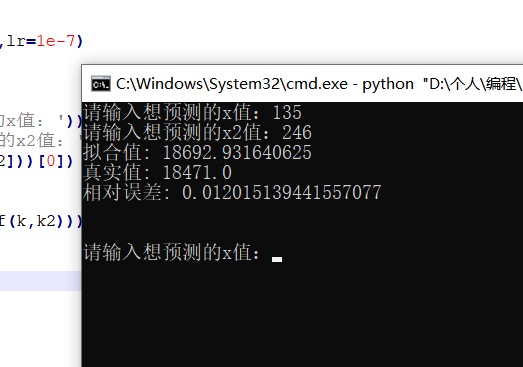
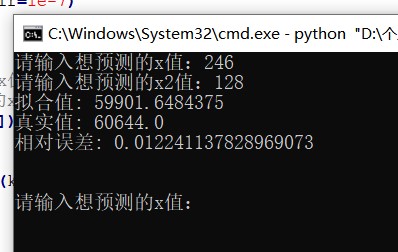
可以看到,这个神经网络拟合的效果还是不错的(拟合误差在2%以内),而且这个神经网络的结构也是比较简单的,如果我们把神经网络的层数增加,神经元的数量增加,那么拟合的效果肯定会更好。
反思
缺点
- 这个神经网络的缺点是,它的结构依旧比较简单。如果我们把神经网络的层数增加,神经元的数量增加,那么拟合的效果肯定会更好。然鹅在训练深度神经网络时,模型的性能随着架构深度的增加而下降。这被称为“退化问题”。这样显然是不划算的。。。。。。
- 出现了过拟合的现象(课本上讲解的过拟合现象)
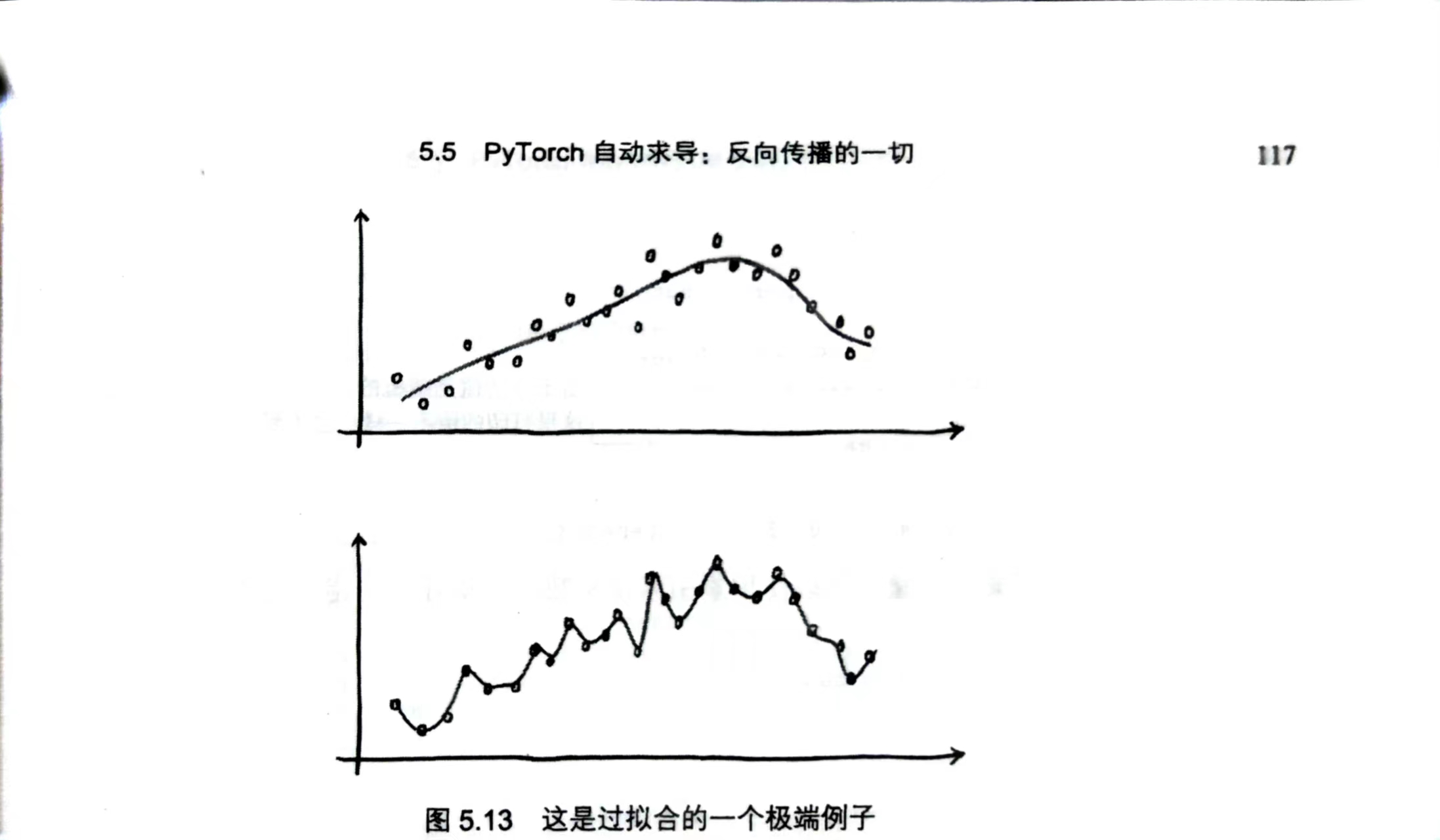
显然,上方的拟合图像才是我们想要的函数图像。
但过多次训练后,这个神经网络的拟合会趋向于下方图像,这就是过拟合的现象。
专业来讲:过拟合现象是指一个模型在训练集上表现优异,但在测试集上表现一般,甚至无法正确预测测试集数据的现象。
所以,这个模型不能过度重复训练,否则会出现过拟合的现象。但是重复训练减少了,又会拟合不足,所以我们需要找到一个平衡点。只能说(道阻且长,行则将至)
优点
- 这个神经网络的优点是,它的结构比较简单,所以训练速度比较快,而且拟合的效果也还不错。
- 这个是前面机器学习的“升 级 版”,构建了前面没有的四层人工神经网络,学习能力更强了。